Functions and Their Graphs
- Calculus 1.1
Functions
A function $f$ is a rule that assigns to each element $x$ in a set $D$ exactly one element $y$ in a set $E$. The set $D$ is called the domain of the function, and the set $E$ is called the codomain of the function. The notation $f(x)=y$ indicates that $y$ is the image of $x$ under the function $f$. The set of all images of elements in the domain is called the range of the function, and is denoted by $Y=f(D)$. The following is the most common representation of a function:
\[ f: X \to Y : x \mapsto f(x) \]
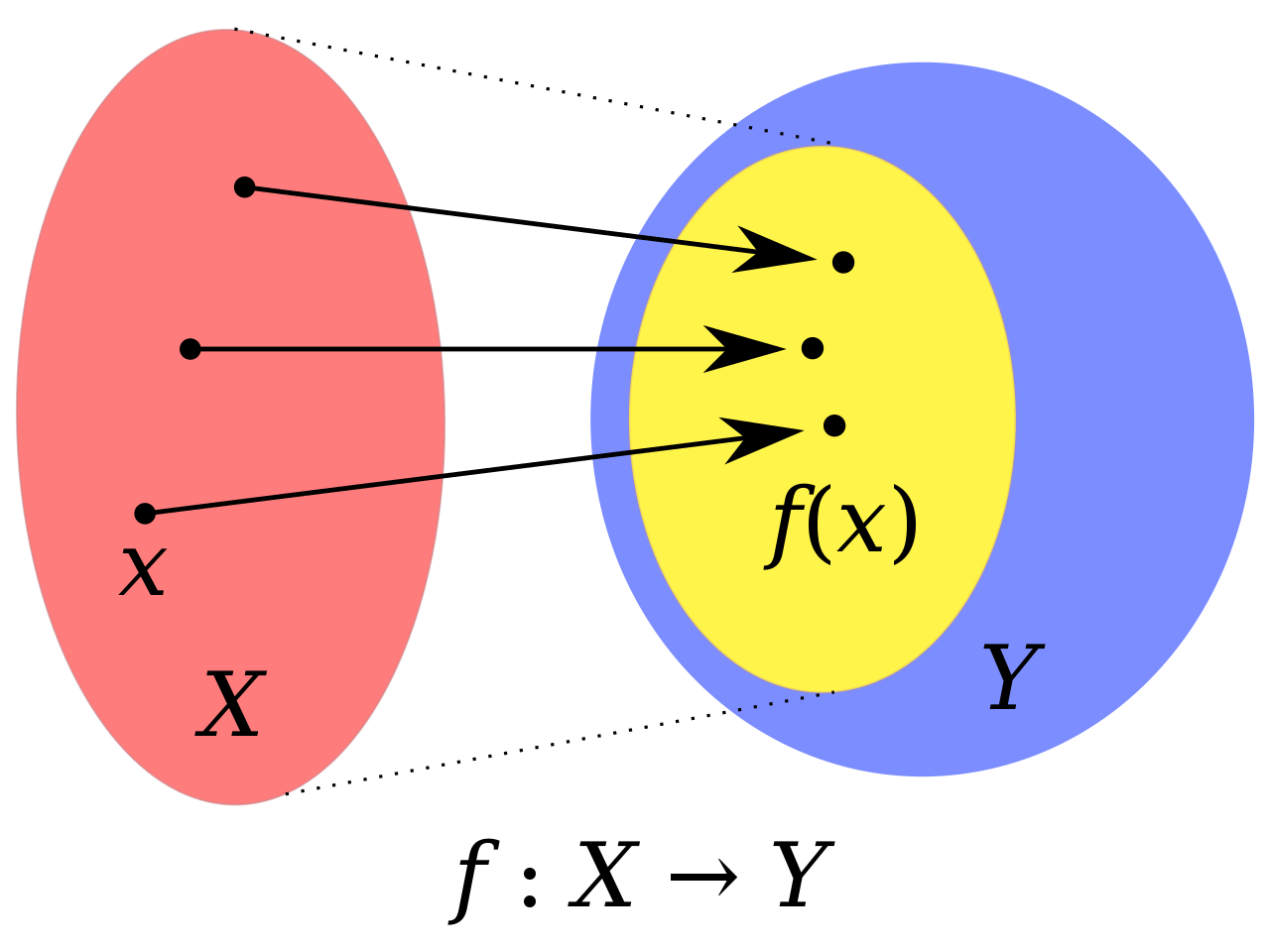
A diagram showing the relationship between the domain, codomain, and range of a function
Often a function is given by a formula that describes how to compute the image of an element in the domain. If the domain is not stated eplicitly, it is assumed to be the largest set for which the formula is defined and this is called the natural domain of the function.
Graphs of Functions
If $y=f(x)$, then the graph of the function is the set of all points $(x,y)$ in the Cartesian plane such that $y$ is the image of $x$ under the function $f$. The graph of a function is a visual representation of the relationship between the domain and range of the function. Graph can be represented in set notation:
\[ G(f) = \set{ (x,f(x)) | x \in D } \subset X\times Y \]

The graph of the sinc function
Increasing and Decreasing Functions
If the graph of a function climbs as we move from left to right, the function is said to be increasing. If the graph falls as we move from left to right, the function is said to be decreasing. Let $f$ be a function defined on an interval $I$, and $x_1,x_2\in I$ two points in the interval.
- If $x_1<x_2 \implies f(x_1)<f(x_2)$, then $f$ is strictly increasing on $I$.
- If $x_1<x_2 \implies f(x_1)>f(x_2)$, then $f$ is strictly decreasing on $I$.
There are also weaker definitions:
- If $x_1<x_2 \implies f(x_1)\leq f(x_2)$, then $f$ is (weakly) increasing on $I$.
- If $x_1<x_2 \implies f(x_1)\geq f(x_2)$, then $f$ is (weakly) decreasing on $I$.
We call a function monotonic if it is either increasing or decreasing on the entire interval.
Even and Odd Functions
The graphs of even and odd functions have special symmetries. A function $y=f(x)$ is
- even if $f(-x)=f(x)$,
- odd if $f(-x)=-f(x)$,
for all $x$ in the domain of $f$.
The graph of an even function is symmetric with respect to the $y$-axis, while the graph of an odd function is symmetric with respect to the origin.
