Skewness and Kurtosis
- Statistics 2.4
Skewness
Skewness $\gamma_1$ is a measure of the asymmetry of the probability distribution of a real-valued random variable. It can be calculated using the formula:
\[ \gamma_1 = \mathrm{E}\left[\left(\frac{X - \mu}{\sigma}\right)^3\right] = \frac{\mu_3}{\sigma^3} \]
where $\mu$ is the mean, $\sigma$ is the standard deviation, and $\mu_3$ is the third central moment of the distribution.
Interpretation of Skewness

Distributions with negative and positive skewness
- Negative Skewness: The left tail is longer or fatter than the right tail. The mass of the distribution is concentrated on the right.
- Positive Skewness: The right tail is longer or fatter than the left tail. The mass of the distribution is concentrated on the left.
- Zero Skewness: The distribution is symmetric, meaning the left and right tails are balanced.
Kurtosis
Kurtosis $\gamma_2$ is a measure of the “tailedness” of the probability distribution of a real-valued random variable. It can be calculated using the formula:
\[ \gamma_2 = \mathrm{E}\left[\left(\frac{X - \mu}{\sigma}\right)^4\right] - 3 = \frac{\mu_4}{\sigma^4} - 3 \]
where $\mu_4$ is the fourth central moment of the distribution. Usually, the value with 3 subtracted is used, so that a normal distribution has a kurtosis of 0, and it is called excess kurtosis. Some sources may use the raw kurtosis value without subtracting 3, which would make the normal distribution have a kurtosis of 3.
Interpretation of Kurtosis
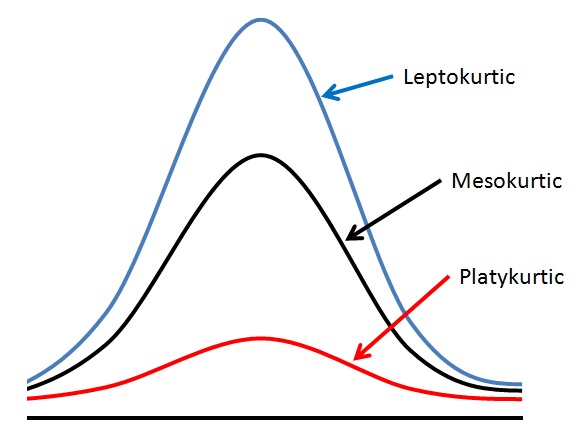
Distributions with negative, positive, and zero kurtosis
- Negative Kurtosis: The distribution has lighter tails than a normal distribution, indicating fewer outliers. It is often referred to as “platykurtic.”
- Zero Kurtosis: The distribution has tails similar to a normal distribution, indicating a moderate level of outliers. It is often referred to as “mesokurtic.”
- Positive Kurtosis: The distribution has heavier tails than a normal distribution, indicating more outliers. It is often referred to as “leptokurtic.”
